Overview

Granular material like sand and dirt is commonplace. Simulating such material is challenging because the behavior of the whole mass depends on the interactions between individual particles. Methods used in engineering, like Discrete Element Method are accurate but very slow, making them non-interactive and unusable for Computer Graphics.

The main behavior contributing to the realistic behavior of granular material is forming piles. An approximate model mimicking this behavior can add significant realism to scenes. The paper titled ”Unified Particle Physics for Real-Time Applications” by Macklin, et. al. proposes a friction model that accounts for relative tangential motion between particles based on friction coefficients and particle penetration distance. The model uses Position Based Dynamics (PBD), a position-based simulation method where particle positions can be updated without an integration step. Although inaccurate, it gives visually plausible results.

Algorithm and Results

The algorithm uses standard position based dynamics to solve constraints:

\(\Delta x_{i}^c = \lambda_i \nabla C(\vec{x})\)
\(\lambda_i = \frac{1}{m_i} \frac{C(\vec{x})}{|\nabla C(\vec{x})|^2}\)

First, we use the distance constraint to resolve inter-particle contacts:

\(C(x_i, x_j) = |x_{ij} - r| \ge 0\)

The gradient of the above constraint is the contact normal: \(\vec{n} = x_i - x_j\)

Once the distance constraints are solved, we handle friction by getting rid part of the relative tangential motion between particles. The first image below shows the initial position of the particles with interpenetration. Gravity pulls the first particle downwards and the collision constraint pushes the particle along the collision vector. The second image shows what could have been the state after collision resolution without friction handling. The friction model proposed by Macklin et. al. calculates the position delta component perpendicular to the collision vector, and decreases it according to chosen friction coefficients and interpenetration distance. This model adds support for static friction by getting rid of the tangential component completely in certain scenarios as described by the model below.

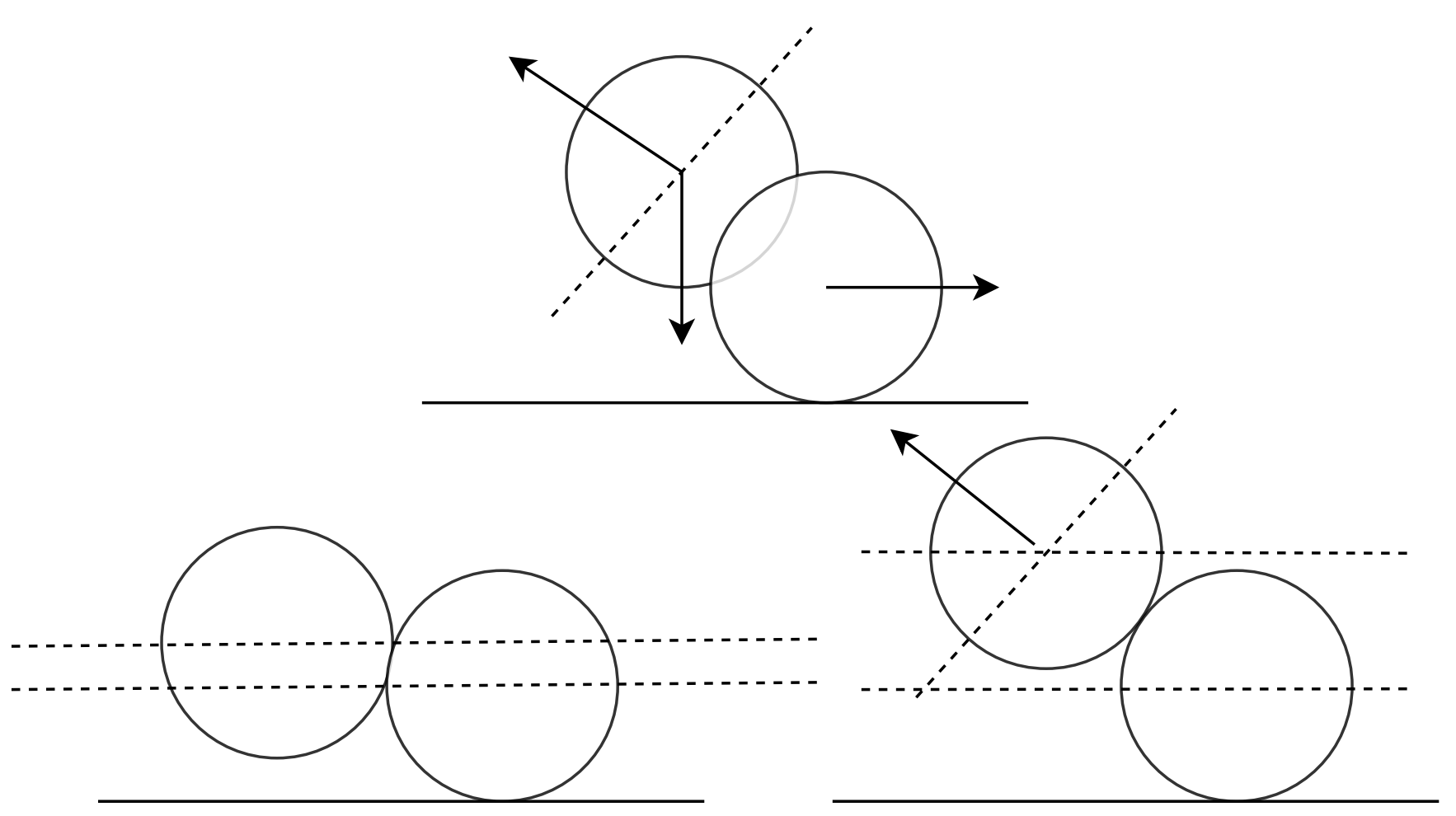
\(\begin{equation} \Delta x_{i}^f = \frac{w_i}{w_i + w_j} \begin{cases} \Delta x_\perp, & |\Delta x_\perp < \mu_s d|\\ \Delta x_\perp \cdot min(\frac{\mu_k d}{\Delta x_\perp}, 1) & \text{otherwise} \end{cases} \end{equation}\)

The final position delta for each particle would be: \(\Delta x = \Delta x_{i}^c + \Delta x_{i}^f\)

Finally we update particles velocities: \(\Delta v = \frac{\Delta x}{\Delta t}\)

Additionally, as proposed by Macklin et. al. we solve the constraints in parallel (on the CPU using OneTBB, in the current implementation) and average the position deltas per particle by dividing the calculated position delta by the number of constraints for that particle:
\(\Delta \tilde{x_i}\ = \frac{1}{n_i} \Delta x_i\)

Collisions with objects

The model proposed by Macklin et. al. handles collisions and friction contact with all objects by representing objects as collections of particles and using the above mentioned contact constraints. This would involve generating tightly packed points on mesh surfaces, and use the above mentioned contact constraints. But, to keep things simple, my implementation handles mesh collisions naively by checking point-triangle intersections. To demonstrate formation of piles, we generate a horizontal grid of particles in place of a floor.

Spatial Hashing

Particle collision detection involves checking particle neighbours for interpenetration. Doing this naively would be to check all particle pairs, resulting in an \(O(n^2)\) operation. For large number of particles this soon becomes intractable. We use spatial hashing to distribute particles on a grid and check particles in the neighbouring grids for collisions. This significantly reduces the number of particle pairs to check. We use the spatial hashing function and algorithm proposed by Matthias Müller: Finding collisions among thousands of objects blazing fast
Here is the used hash function:

    xi = floor(px / grid size)
    yi = floor(px / grid size)
    zi = floor(px / grid size)

    hashCoords(xi, yi, zi) {
        h = (xi * 92837111) ^ (yi * 689287499) ^ (zi * 283923481)
        return abs(h) % numberOfCells
    }

Generating particle clusters and rendering with Blender

To demonstrate different visual results we generate grains in the volume of meshes. Blender’s geometry nodes allows us to visually program geometric manipulations. This is much faster than using python scripts in Blender since geometry nodes are implemented in C++ under the hood. We use the following geometry node setup (from Ducky 3D’s YouTube tutorial: Filling objects is easy now) to generate particles inside meshes. Although not tightly packed, it gives visually reasonable results.

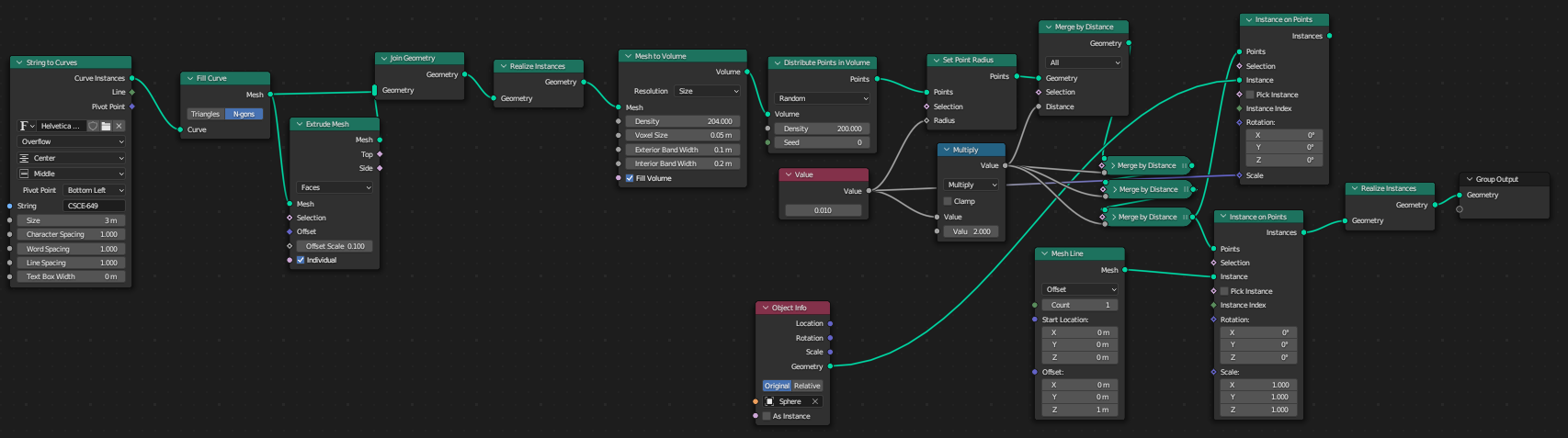
    generate points in mesh:
        convert mesh to volume (voxelize mesh)
        generate points in volume
        for i in 1...4
            merge points within distance of 2 * particleRadius

To improve the visual quality of the final results we export particle positions to blender and use the Cycles rendering engine for final images:

Export per-timestep list of points from simulator to a text file
Convert list of points to per-timestep ply files using a python script
Use a blender python script to import ply files for each frame, and keyframe object visibility per-frame (since you cannot explicitly import objects for each frame)

Results

Dam break simulations eventually form piles of grains as expected.

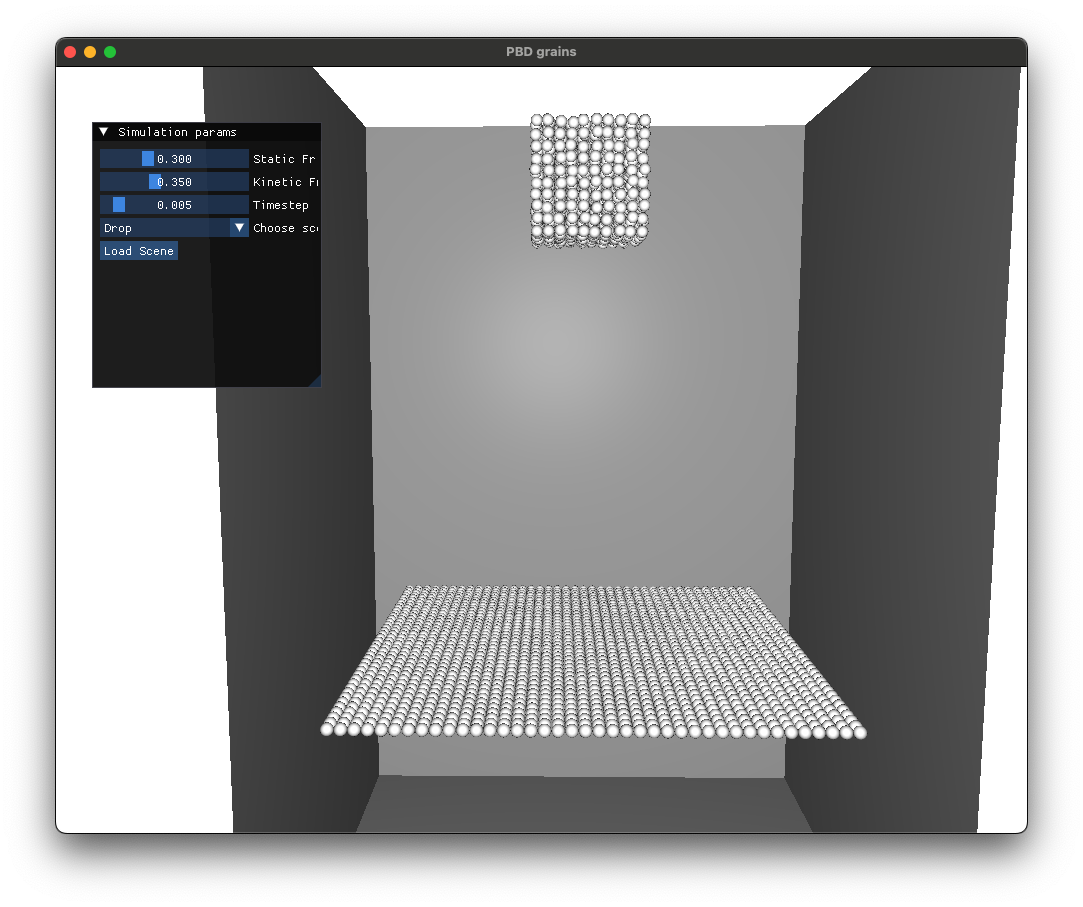
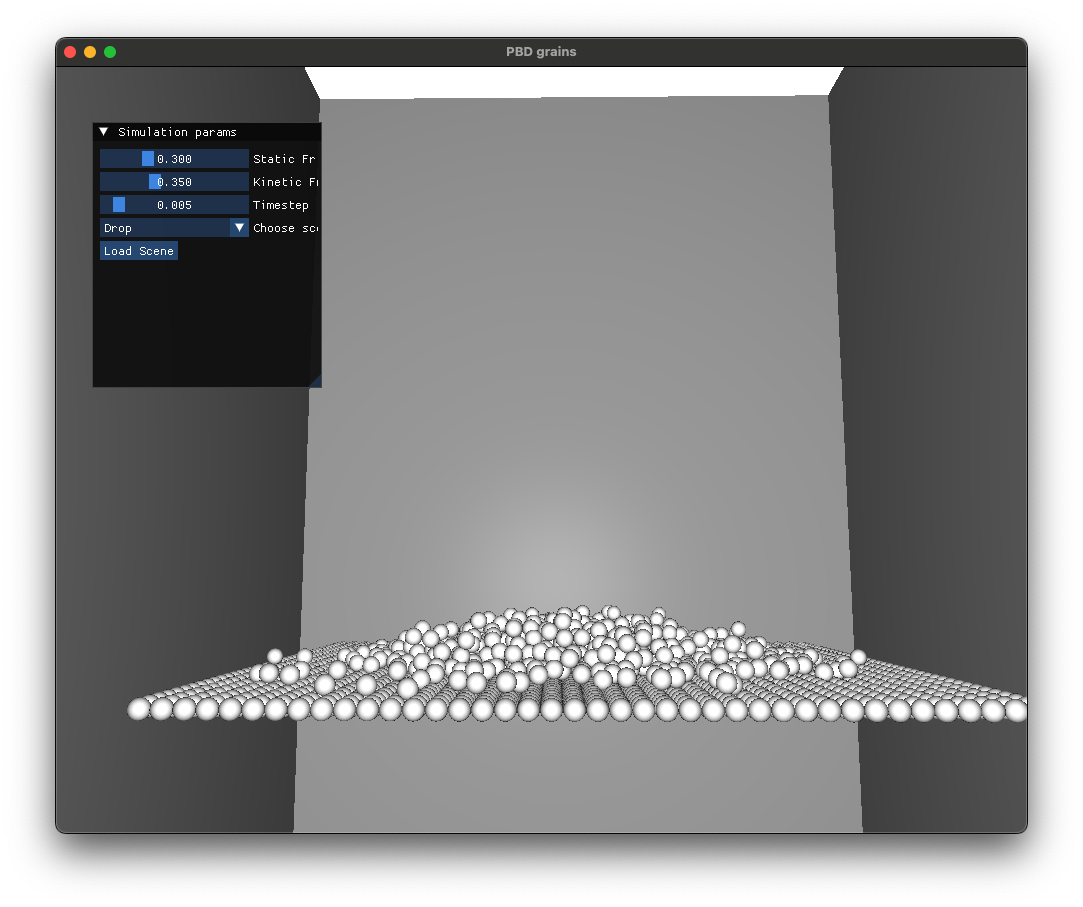
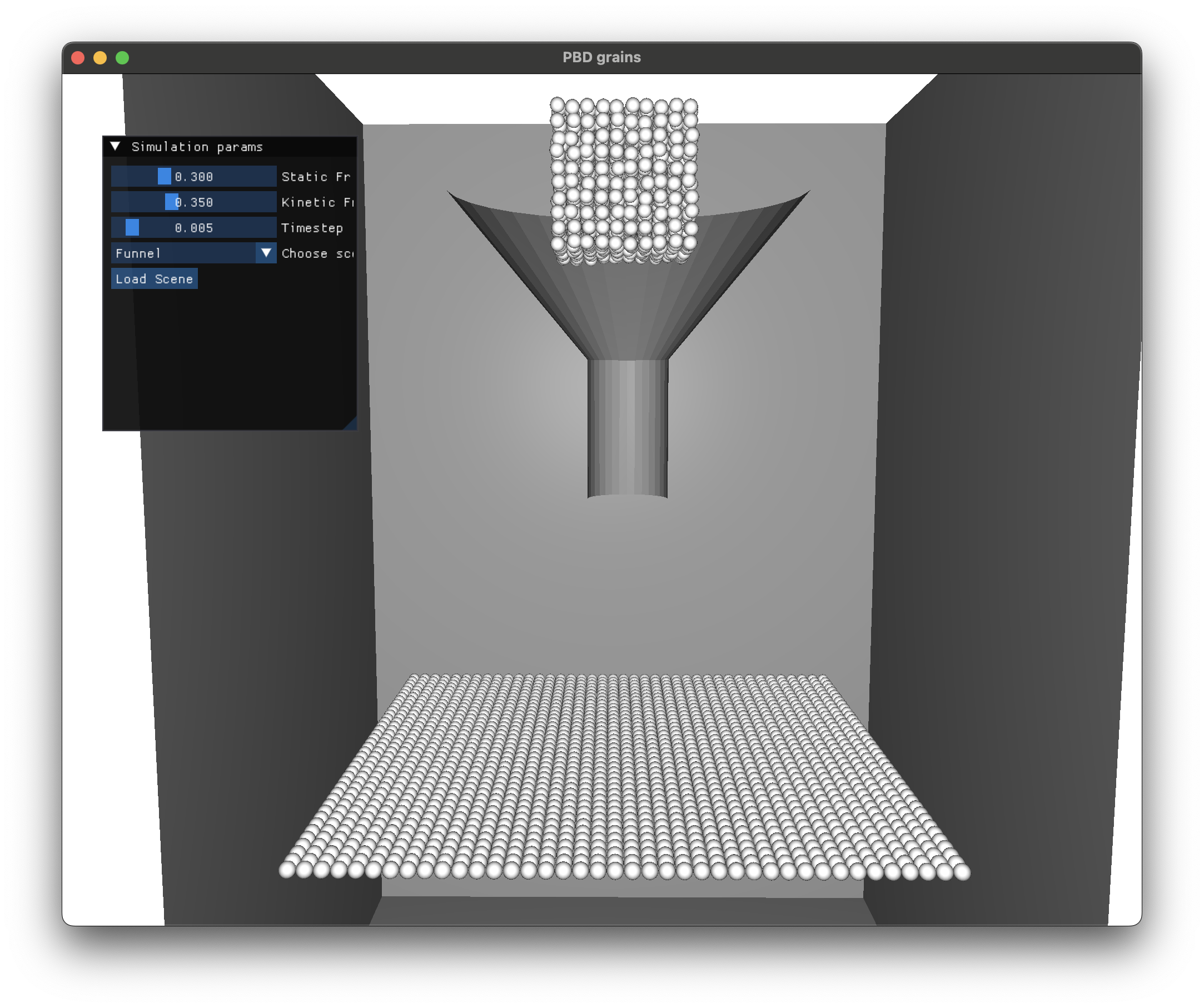
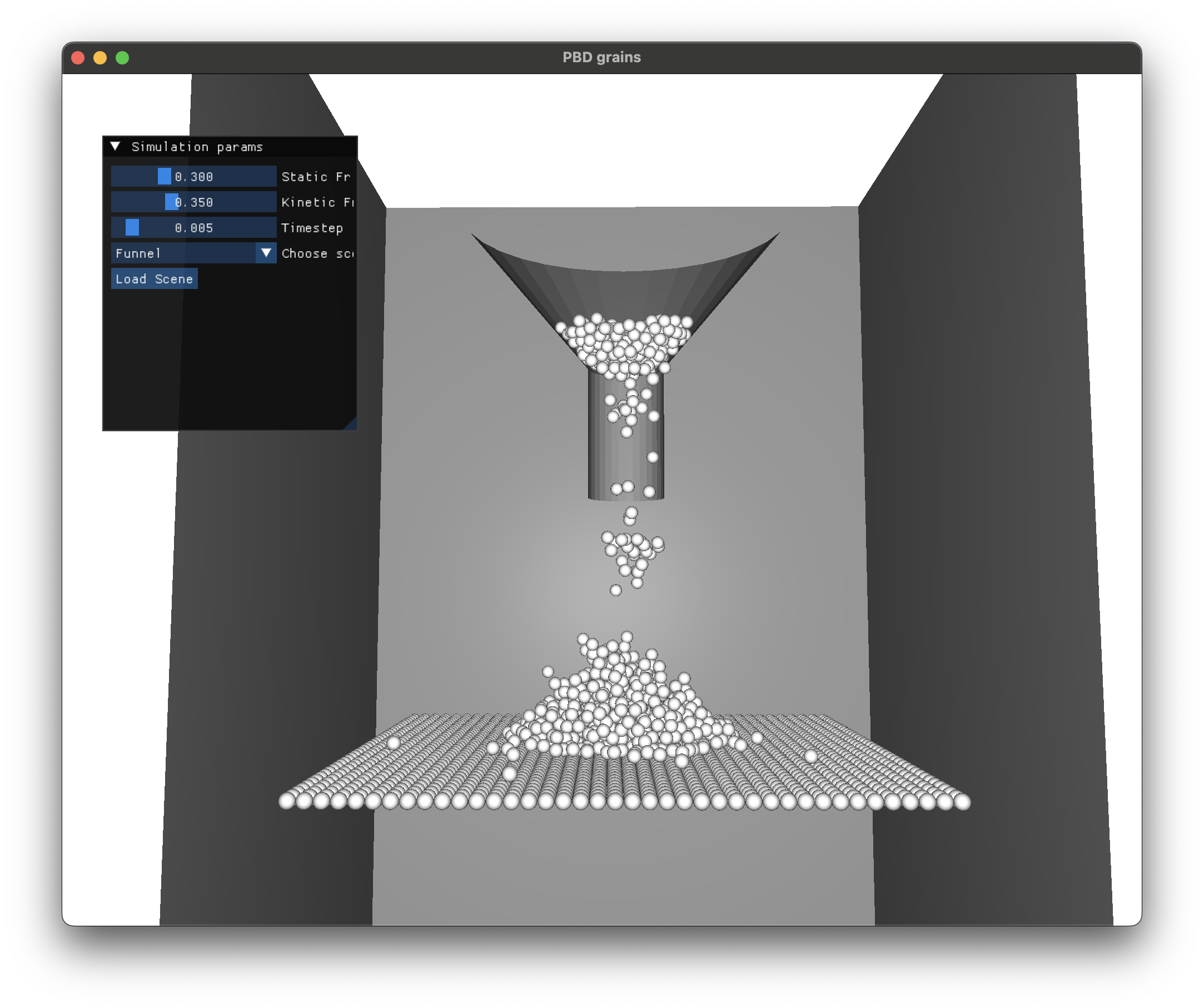
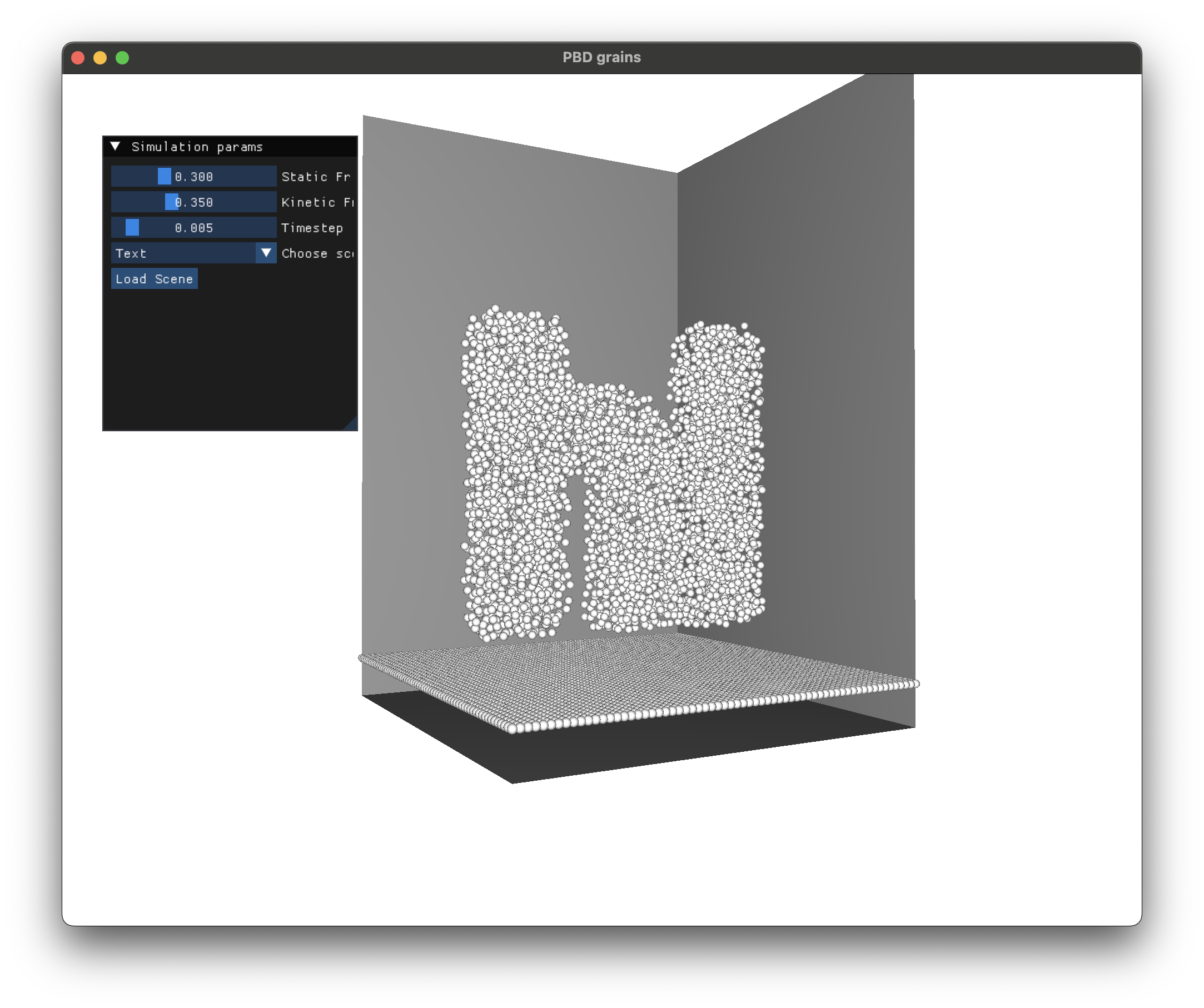
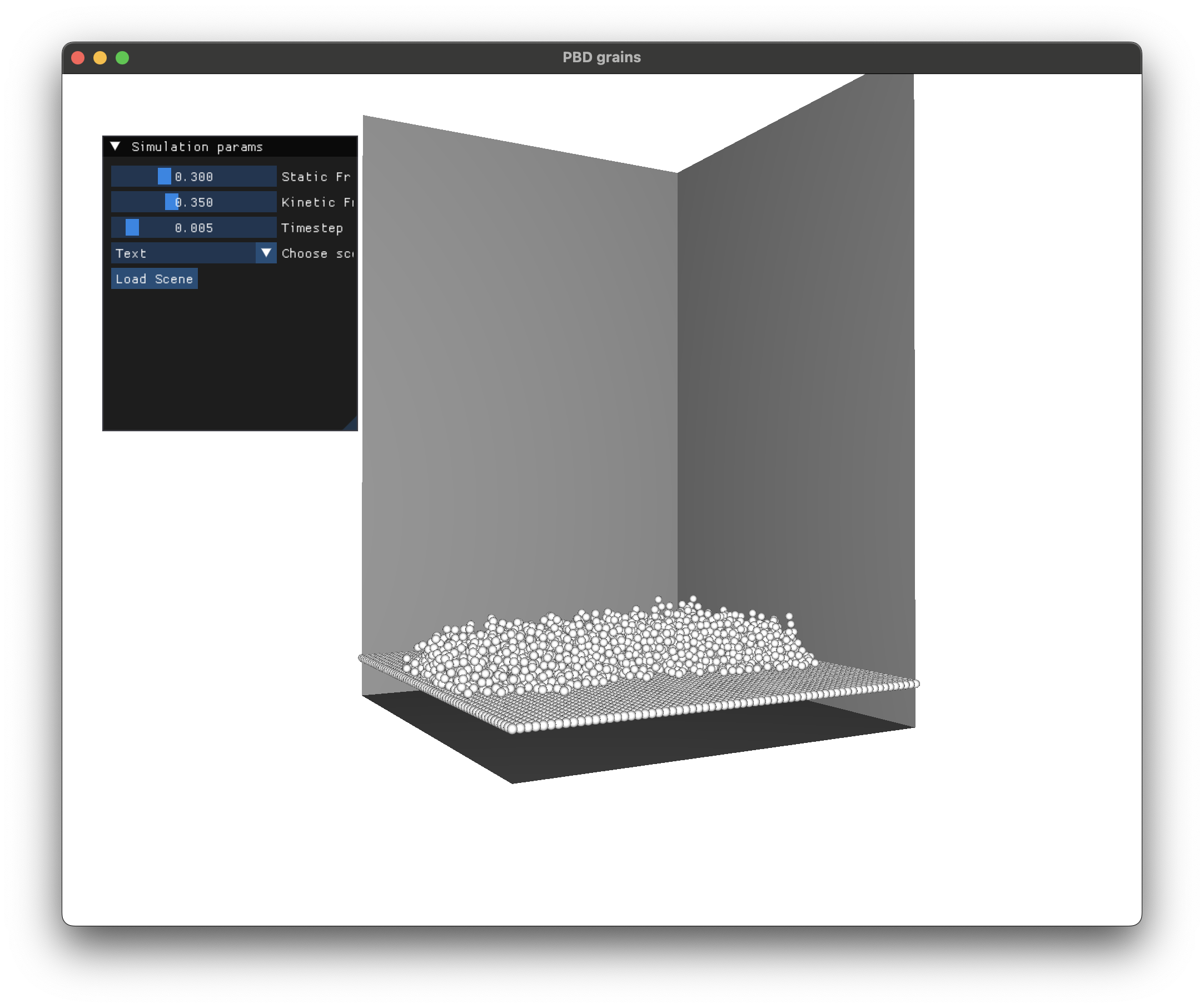
Code Repository

GitHub Repo: pbd-grains

Acknowledgements

The OpenGL boilerplate code has been borrowed from Prof. Sueda’s assignment material and has been modified for OpenGL 4.x.
The project is based on the papers: “Unified Particle Physics for Real-Time Applications” by Macklin, et.al.
GLM and Eigen were used for vector math
oneTBB was used for multi-threading
Spatial hashing algorithm by Matthias Müller: Finding collisions among thousands of objects blazing fast
Ducky 3D’s YouTube tutorial: Filling objects is easy now

Granular Simulation with Position Based Dynamics